位置エネルギーの定義
仕事と保存力
位置 \(\boldsymbol{r}\) にある物体に力 \(\boldsymbol{F}(\boldsymbol{r})\) が働いている状況を考えます.
力が働くことによって物体の位置は移動していき,何らかの運動の軌跡を描きます.
この運動の軌跡を $C$ とすると,この力が物体になす仕事 \(W\) は,
と定義されます.
仕事は一般に積分する経路 $C$ に依存しますが,その道筋に依存せず,経路の始点と終点にのみ依存する場合があります.
このように,仕事が始点と終点にのみ依存するとき,その力を保存力と言います.
位置エネルギーの導入
力が保存力のとき,仕事は始点 \(\boldsymbol{r}_0\) と 終点 \(\boldsymbol{r}\) にのみ依存するので,次のように書けます:
ここで,\(U(\boldsymbol{r})\) というスカラー関数(スカラー場)を導入しました.
この \(U(\boldsymbol{r})\) のことを位置エネルギーと言います.
位置エネルギーの物理的意味
一様重力を例に,位置エネルギーの物理的な意味について説明します.
例:一様重力による位置エネルギー
地表を原点として,鉛直上向きを正に \(z\) 軸を取ります.
このとき,質量 \(m\) の物体に働く一様重力 \(\boldsymbol{F}\) は,
と表されます.
\(g\) は重力加速度の大きさです.
一様重力は,\(z\) 方向の成分しか持たず,さらにその成分は位置に依存せず一定なため,その仕事は経路に依らずに始点と終点の「高さ」の差のみに依存します:
よって,一様重力は保存力であることがわかります.
そして,一様重力による位置エネルギーは,
と与えられます.
ここで,\(C\) はエネルギーの次元をもつ任意定数です.
\(C\) は位置エネルギーの基準を定めるもので,いまは \(C=0\) と取ります.
このことは,地表を位置エネルギーの基準に取ることに対応します.
すると,
となります.
グラフに表すと,以下のような直線になります.
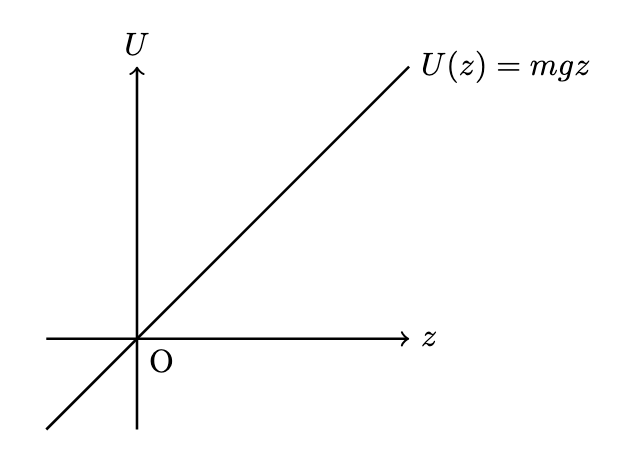
位置エネルギーの意味とは?
一様重力の位置エネルギー \(U(z)=mgz\) を用いて位置エネルギーの意味について説明します.
この位置エネルギーは地表からの高さ \(z\) に応じてその値が決まり,高ければ高いほど(\(z\) が大きいほど)その値は大きくなります.
このことは,物体が高い位置にあるほど、重力によってより大きな仕事をし得る状態にあることを意味しています.
すなわち,位置エネルギーとは,物体がその位置にあることで潜在的にもつエネルギーのことです.
位置エネルギーから一様重力の導出
最後に,位置エネルギー \(U(z)=mgz\) から 一様重力 \(\boldsymbol{F}=-mg\boldsymbol{e}_z\) を導きます.
\(U(z)=mgz\) を \(z\) について微分して,基底ベクトル \(\boldsymbol{e}_z\) をかけて,さらに \((-1)\) 倍すれば,一様重力が得られます:








