目次
力学変数(一般化座標)
力学変数(一般化座標)とは、各時刻 \(t\) における系の状態を一意的に指定する変数です
\(N\) 個の独立な力学変数で記述される系を \(N\) 自由度系と言います。
例えば、
- 3 次元空間中を運動する 1 質点系は、1 つの位置ベクトルで状態を指定でき、その独立な成分の数は 3 つなので、\(N=3\)
- 3 次元空間中を運動する 2 質点系は、位置ベクトルが 2 つ必要なので、 \(N=3\times 2=6\)
となります。
ここで、力学変数はあくまでも各時刻 \(t\) での系の状態を決める変数であることに注意してください。
例えば、ある時刻における位置を決めただけでは、あらゆる方向に運動することができ(速度が決まっておらず)、時間発展したあとの系の状態は一意に定まりません。
Newton 力学で学んだように、ある時刻における位置と速度を与えて運動方程式を解くことで、系の時間発展が決まります
そして、
力学変数(一般化座標)は必ずしも座標とは限りません!
解析力学(正確には場の理論)で電磁場を定式化することができるのですが、その際は、スカラーポテンシャル \(\phi(\boldsymbol{x},t)\) とベクトルポテンシャル \(\boldsymbol{A}(\boldsymbol{x},t)\) が力学変数となります
Lagrange 形式による定式化
解析力学を Lagrange 形式で定式化するために、ラグランジアンと最小作用の原理について説明します。
ラグランジアン
\(N\) 個の独立な力学変数 \(q_i(t)\) \((i=1,2,\dots,N)\) で記述される \(N\) 自由度系を考えます。
このとき、ラグランジアンと呼ばれる量を次のように導入します。
ラグランジアン
\begin{align}
L
=&L(q_1(t),q_2(t),\dots,q_N(t),\dot{q}_1(t),\dot{q}_2(t),\dots,\dot{q}_N(t),t)\notag\\
=&L(q(t),\dot{q}(t),t)
\end{align}
ここで、
\begin{align}
\dot{q}_i(t)=\frac{dq_i(t)}{dt}
\end{align}
を定義し、また、
\begin{align}
q(t)=&(q_1(t),q_2(t),\dots,q_N(t)),\\
\dot{q}(t)=&(\dot{q}_1(t),\dot{q}_2(t),\dots,\dot{q}_N(t))
\end{align}
のように \(N\) 個の変数をまとめて表す表記を導入しました。
このラグランジアンは系固有のものであり、次に説明する最小作用の原理により、系の時間発展が決定します。
その前に、ラグランジアンについていくつかコメントをしておきます
- ラグランジアンは力学変数 \(q(t)\) とその時間についての 1 階微分 \(\dot{q}(t)\) の関数で、2 階以上の微分は含まないとします。これは、Newton の運動方程式が位置を変数とする 2 階微分方程式であることによる自然な推測です。
- 空間並進対称性やゲージ対称性などの対称性を原理としてラグランジアンの具体的な関数形を制限することができ、この手法は素粒子論などの現代物理学において有用です。
- ポテンシャル \(U\) 中を運動する質点系(保存力下の質点系)に対して、ラグランジアンは \(L=T-U\) で与えられます。\(T\) は運動エネルギーです。
- \(L=L(q(t),\dot{q}(t),t)\) の最後の変数 \(t\) は、\(q(t), \dot{q}(t)\) を通じた以外の時間依存性を表しています。この時間依存性を陽な時間依存性と言います。エネルギーが保存する系ではラグランジアンは陽な時間依存性をもたないです。このことを陰に時間に依存していると言います。
エネルギーが保存しない例として、強制振動が挙げられます。
最小作用の原理
ラグランジアンを導入したので、次に最小作用の原理を説明します。
最小作用の原理
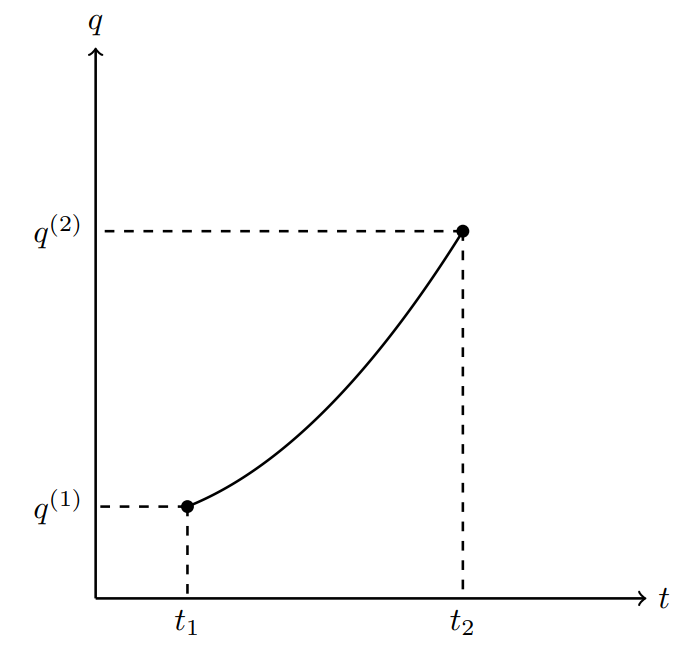
時刻 \(t=t_1, t_2\) (\(t_1<t_2\)) において、力学変数 \(q(t)\) の値が定まっているとします。
\begin{align}
q(t_1)=q^{(1)},\quad q(t_2)=q^{(2)}.
\end{align}
このとき、\(t_1<t<t_2\) における系の時間発展は、作用
\begin{align}
S[q]=\int_{t_1}^{t_2}dt L(q(t),\dot{q}(t),t)
\end{align}
を最小に(正確には、停留)するように決まります。
 作用を停留させるような軌道
作用を停留させるような軌道
最小作用の原理は解析力学の枠組みにおける基本原理であり、何かから導出されるものではありません!
この原理から予言される物理的な帰結を観測によって裏付けることで、理論の正当性が保証されます
ここで導入した作用 \(S[q]\) は、力学変数 \(q(t)\) を与えると数を返す量(つまり「関数 \(q(t)\) の関数」)であり、汎関数と呼ばれます。
Newton 力学における運動方程式は、最小作用の原理により導くことができます。
このことについて、これから説明します。
Euler-Lagrange 方程式
最小作用の原理から、力学変数 \(q(t)\) に対する微分方程式、つまり、運動方程式を導きます。
この運動方程式を Euler-Lagrange 方程式と呼びます。
Euler-Lagrange 方程式
\begin{align}
\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_i}-\frac{\partial L}{\partial q_i}=0\qquad(i=1,2,\dots,N)
\end{align}
Euler-Lagrange 方程式の導出
Euler-Lagrange 方程式を導出します。
まず、\(q(t)\) が最小作用の原理を満たす時間 \(t\) の関数とします。
つまり、\(q(t)\) は境界条件
\begin{align}
q(t_1)=q^{(1)},\quad q(t_2)=q^{(2)}
\end{align}
を満たし、作用 \(S[q]\) を停留させるとします。
この \(q(t)\) から任意の微小関数 \(\delta q(t)\) だけずれた関数
\begin{align}
q(t)+\delta q(t)
\end{align}
を考えます。
この \(\delta q(t)\) を \(q(t)\) の変分と言います
\(q(t)+\delta q(t)\) も境界条件を満たすことから、\(\delta q(t_1)=\delta q(t_2)=0\) が従います
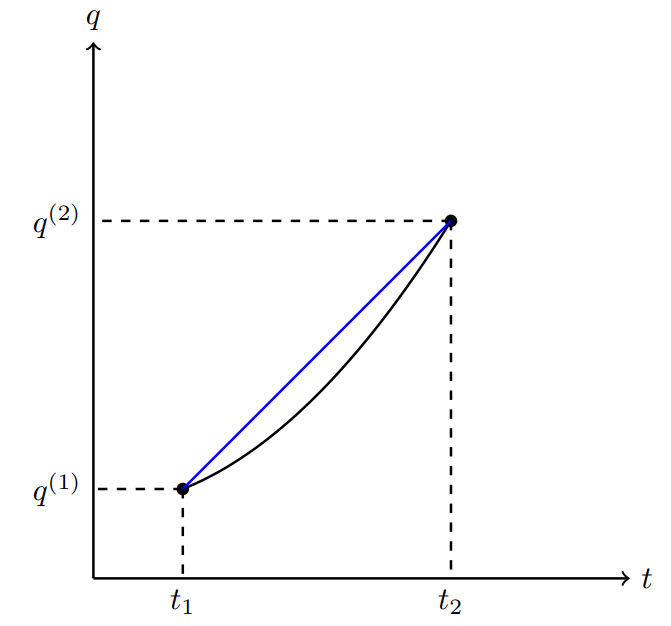
 黒が作用を停留させる軌道のとき、青がその軌道から微小だけずれた軌道の例
黒が作用を停留させる軌道のとき、青がその軌道から微小だけずれた軌道の例
\(q(t)\) が作用 \(S[q]\) を停留させるとは、\(q(t)+\delta q(t)\) に対する作用 \(S[q+\delta q]\) を任意の微小関数 \(\delta q(t)\) について冪展開したときに、その 1 次の項の係数がゼロということです。
0 次の項が自然とキャンセルするように、次の量でこの条件を計算します。
\begin{align}
S[q+\delta q]-S[q]
=&\int_{t_1}^{t_2}dt L(q+\delta q,\dot{q}+\delta \dot{q},t)\notag\\
&-\int_{t_1}^{t_2}dt L(q,\dot{q},t)\notag\\
\simeq&\int_{t_1}^{t_2}dt \left(L(q,\dot{q},t)+\frac{\partial L(q,\dot{q},t)}{\partial q_i}\delta q_i+\frac{\partial L(q,\dot{q},t)}{\partial \dot{q}_i}\delta \dot{q}_i\right)\notag\\
&-\int_{t_1}^{t_2}dt L(q,\dot{q},t)\notag\\
=&\int_{t_1}^{t_2}dt \left(\frac{\partial L(q,\dot{q},t)}{\partial q_i}\delta q_i+\frac{\partial L(q,\dot{q},t)}{\partial \dot{q}_i}\delta \dot{q}_i\right)\notag\\
=&\int_{t_1}^{t_2}dt \left(\frac{\partial L(q,\dot{q},t)}{\partial q_i}\delta q_i+\frac{\partial L(q,\dot{q},t)}{\partial \dot{q}_i}\frac{d}{dt}\delta q_i\right)\notag\\
=&\int_{t_1}^{t_2}dt \left(\frac{\partial L(q,\dot{q},t)}{\partial q_i}-\frac{d}{dt}\frac{\partial L(q,\dot{q},t)}{\partial \dot{q}_i}\right)\delta q_i\notag\\
&+\left[\frac{\partial L(q,\dot{q},t)}{\partial \dot{q}_i}\delta q_i\right]_{t=t_1}^{t_2}.
\end{align}
1 つ目の等号では、作用の定義を代入しました。
2 つ目の等号(近似記号)では、第 1 項を \(q, \dot{q}\) の周りで冪展開して、\(\delta q, \delta\dot{q}\) の 2 次以上の項を無視しました。
また、和の記号 \(\sum_{i=1}^{N}\) を省略する Einstein の規約を用いました。
3 つ目の等号では、0 次の項をキャンセルしました。
4 つ目の等号では、
\begin{align}
\delta \dot{q}_i(t)=\frac{d}{dt}\delta q_i(t)
\end{align}
を用いました。
5 つ目の等号では、第 2 項を部分積分しました。
その表面項は境界条件 \(\delta q(t_1)=\delta q(t_2)=0\) からゼロになります。
\begin{align}
\left[\frac{\partial L(q,\dot{q},t)}{\partial \dot{q}_i}\delta q_i\right]_{t=t_1}^{t_2}=0.
\end{align}
よって、
\begin{align}
S[q+\delta q]-S[q]
\simeq\int_{t_1}^{t_2}dt \left(\frac{\partial L(q,\dot{q},t)}{\partial q_i}-\frac{d}{dt}\frac{\partial L(q,\dot{q},t)}{\partial \dot{q}_i}\right)\delta q_i
\end{align}
が得られます。
\(\delta q_i\) は任意なので、作用を停留させる条件より、
\begin{align}
\frac{d}{dt}\frac{\partial L(q,\dot{q},t)}{\partial \dot{q}_i}-\frac{\partial L(q,\dot{q},t)}{\partial q_i}=0\qquad(i=1,2,\dots,N)
\end{align}
が従います。
これがEuler-Lagrange 方程式です。
各 \(i\) に対して、微分方程式が得られることに注意してください
また、\(S[q+\delta q]-S[q]\) のうち、\(\delta q\) の 1 次の項を \(S[q]\) の変分と言い、\(\delta S[q]\) と書きます。
\begin{align}
\delta S[q]=\int_{t_1}^{t_2}dt \left(\frac{\partial L(q,\dot{q},t)}{\partial q_i}-\frac{d}{dt}\frac{\partial L(q,\dot{q},t)}{\partial \dot{q}_i}\right)\delta q_i.
\end{align}
\(S[q]\) の変分を用いると、最小作用の原理は、任意の \(\delta q\) に対して、
\begin{align}
\delta S[q]=0
\end{align}
と書くこともできます。
この条件式から Euler-Lagrange 方程式を導く手法を変分法と言います
最小作用の原理は変分原理とも呼ばれます
Euler-Lagrange 方程式の具体例:ポテンシャル中の 1 質点系
最小作用の原理から Euler-Lagrange 方程式を導くことができたので、その具体例を 1 つ紹介します。
3 次元空間を運動する 1 質点系を考え、その質点の質量を \(m\)、位置を \(\boldsymbol{r}(t)=(x_1(t),x_2(t),x_3(t))\) とします。
\begin{align}
q_i(t)=x_i(t)\qquad(i=1,2,3)
\end{align}
質点に働く力はポテンシャル \(U(\boldsymbol{r}(t))\) によるもののみとします。
この系のラグランジアンは、
\begin{align}
L(\boldsymbol{r}(t),\dot{\boldsymbol{r}}(t))
=\frac{1}{2}m\dot{\boldsymbol{r}}(t)^2-U(\boldsymbol{r}(t))
\label{Lexam}
\end{align}
で与えられます。
Euler-Lagrange 方程式に代入して、この系の運動方程式を求めます。
Euler-Lagrange 方程式はベクトルを用いた表記で、
\begin{align}
\frac{d}{dt}\frac{\partial L}{\partial \dot{\boldsymbol{r}}}-\frac{\partial L}{\partial \boldsymbol{r}}=\boldsymbol{0}
\label{eomvec}
\end{align}
となります。
ここで、
\begin{align}
\frac{\partial}{\partial \boldsymbol{r}}=&\boldsymbol{\nabla}=\left(\frac{\partial}{\partial x_1}, \frac{\partial}{\partial x_2}, \frac{\partial}{\partial x_3}\right),\\
\frac{\partial}{\partial \dot{\boldsymbol{r}}}=&\left(\frac{\partial}{\partial \dot{x}_1}, \frac{\partial}{\partial \dot{x}_2}, \frac{\partial}{\partial \dot{x}_3}\right)
\end{align}
です。
\eqref{Lexam} を \eqref{eomvec} に代入すると、
\begin{align}
\boldsymbol{0}
=&\frac{d}{dt}\frac{\partial L}{\partial \dot{\boldsymbol{r}}}-\frac{\partial L}{\partial \boldsymbol{r}}\notag\\
=&\frac{d}{dt}(m\dot{\boldsymbol{r}})+\frac{\partial U(\boldsymbol{r})}{\partial \boldsymbol{r}}\notag\\
=&m\ddot{\boldsymbol{r}}+\boldsymbol{\nabla}U(\boldsymbol{r})
\end{align}
となります。
これを整理すると、
\begin{align}
m\ddot{\boldsymbol{r}}=-\boldsymbol{\nabla}U(\boldsymbol{r})
\end{align}
となり、Euler-Lagrange 方程式から、ポテンシャル中を運動する 1 質点系が従う Newton の運動方程式が得られます。
\(\boldsymbol{r}\) と \(\dot{\boldsymbol{r}}\) は互いに独立な変数として扱います
\begin{align}
\end{align}