【力学】位置・速度・加速度の導入

力学の基本的な目標の一つは，ある時刻における物体の状態（位置や速度など）をもとに，任意の時刻における運動を予測することです．

以下の記事で，物体の位置を特定するために必要な要素の数である自由度と，それを測るための座標系について説明しました．

この記事では，座標系においてどのように位置が表現されるかを述べます．

また，速度と加速度を導入し，物体の運動を調べる準備を進めます．

位置・速度・加速度

簡単のため，1 次元運動を考えます．

1 次元運動とは，自由落下運動のような直線的な運動のことです．

位置

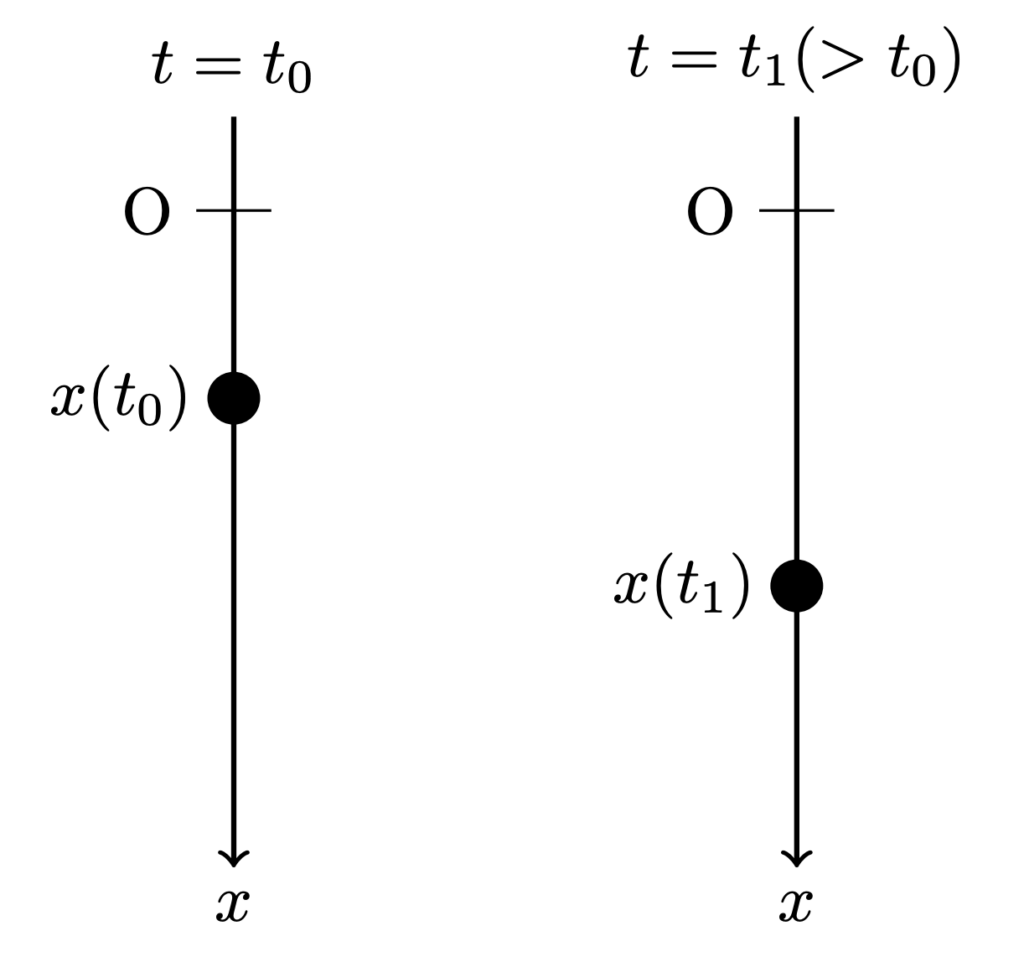
1 次元運動における質点の位置 $x$ は，その直線上に適当に原点 O を取り，向きづけした数直線によって測ることができます．

この数直線を $x$ 軸と呼ぶことにします．

$x$ 軸は向きづけされているので，原点から測った質点の位置は正負どちらの値も取り得ることになります．

また一般に，質点の位置は時間 $t$ とともに変化します．

つまり，位置 $x$ は時刻 $t$ の関数として表されます：

速度

ある時刻 $t=t_0$ とそれより後の時刻 $t=t_1(>t_0)$ における位置はそれぞれ，$x(t_0),x(t_1)$ と表されます．

これらの位置の変化分（変位）$x(t_1)-x(t_0)$ を時間差 $t_1-t_0$ で割った量を，時刻 $t_0$ から $t_1$ までの間の 平均速度と言います：

時刻 $t_1=t_0+\Delta t$ とおくと，

さらに $t_0$ を $t$ と書き，$\Delta t\to0$ の極限を取ると，

これを時刻 $t$ における瞬間速度と言い，$v(t)$ と書きます：

定義により，位置の時間に関する 1 階微分が速度です：

位置と同様に，速度の値も正負どちらにもなり得ます．

また，速度の大きさ（絶対値） $|v(t)|$ を時刻 $t$ における速さと言います．

加速度

一般に速度 $v(t)$ も時間 $t$ とともに変化します．

この変化の度合いを加速度と言います．

時刻 $t$ から $t+\Delta t$ までの間の平均加速度を，

と定義します．

また，時刻 $t$ における瞬間加速度 $a(t)$ を，

と定義します．

加速度は速度の時間に関する 1階微分であり，位置の 2 階微分です：