目次
問題設定
重力加速度を $\boldsymbol{g}$ ,その大きさを $g$ とします.
抵抗力の比例定数を $\gamma$ とします.
質点の質量を $m$ ,時刻 $t$ における位置を $\boldsymbol{r}(t)$ ,速度を $\boldsymbol{v}(t)$ とします.
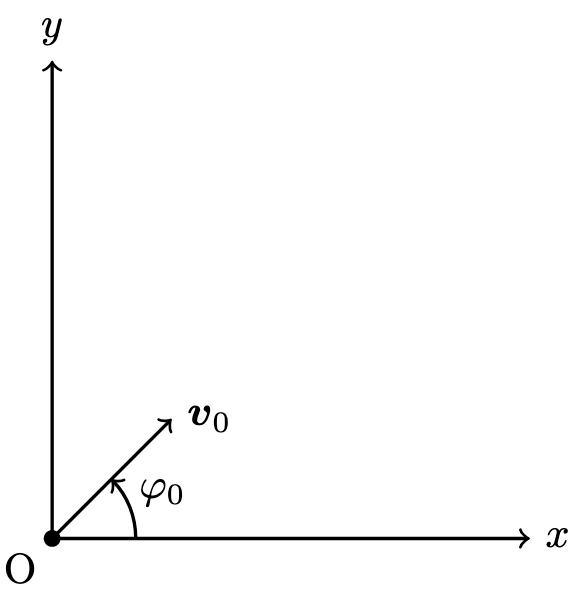
座標系は図のように取ります.

このとき,ベクトル量を次のように成分表示します:
\begin{align}
\boldsymbol{g}&=(0,-g),\\
\boldsymbol{r}(t)&=(x(t),y(t)),\\
\boldsymbol{v}(t)&=(v_x(t),v_y(t)).
\end{align}
時刻 $t=0$ における初期条件は,
\begin{align}
\boldsymbol{r}_0&=\boldsymbol{r}(0)=(x(0),y(0))=(0,0),\\
\boldsymbol{v}_0&=\boldsymbol{v}(0)=(v_x(0),v_y(0))=(v_0\cos{\varphi_0},v_0\sin{\varphi_0}).
\end{align}
問題
(1)$x$ 方向,$y$ 方向の運動方程式をそれぞれ立てよ.
(2)$x$ 方向の運動方程式を解け.
(3)$y$ 方向の運動方程式を解け.
解答
(1)$x$ 方向,$y$ 方向の運動方程式をそれぞれ立てよ.
質点に働く力は重力と速度に比例した抵抗力なので,運動方程式は,
\begin{align}
m\frac{d\boldsymbol{v}(t)}{dt}=m\boldsymbol{g}-\gamma\boldsymbol{v}(t).
\end{align}
鉛直上向きに $y$ 軸の正の向きを取っているので,重力は,
\begin{align}
m\boldsymbol{g}=(0,-mg)
\end{align}
となります.
よって,$x$ 方向,$y$ 方向の運動方程式はそれぞれ,
\begin{align}
m\frac{dv_x(t)}{dt}&=-\gamma v_x(t),\\
m\frac{dv_y(t)}{dt}&=-mg-\gamma v_y(t)
\end{align}
となります.
(2)$x$ 方向の運動方程式を解け.
\begin{align}
m\frac{dv_x(t)}{dt}&=-\gamma v_x(t)
\end{align}
を変数分離法を用いて解きます.
左辺に $v_x(t)$ ,右辺に $t$ を集めると,
\begin{align}
\frac{dv_x(t)}{v_x(t)}&=-\frac{\gamma}{m}dt.
\end{align}
この両辺を積分すると,
\begin{align}
\int_{v_x(0)}^{v_x(t)}\frac{dv_x}{v_x}&=-\frac{\gamma}{m}\int_{0}^{t}dt\\
\log\frac{v_x(t)}{v_x(0)}&=-\frac{\gamma}{m}t\\
v_x(t)&=v_x(0)\exp\left[-\frac{\gamma}{m}t\right].
\end{align}
初期条件 $v_x(0)=v_0\cos{\varphi_0}$ を用いると,$x$ 方向の速度は,
\begin{align}
v_x(t)=v_0\cos{\varphi_0}\exp\left[-\frac{\gamma}{m}t\right]
\end{align}
となります.
さらに,この式の両辺を $t$ で積分すると,
\begin{align}
\int_{0}^{t}v_x(t’)dt’&=v_0\cos{\varphi_0}\int_{0}^{t}\exp\left[-\frac{\gamma}{m}t’\right]dt’\\
x(t)-x(0)&=\frac{mv_0\cos{\varphi_0}}{\gamma}\left(1-\exp\left[-\frac{\gamma}{m}t\right]\right).
\end{align}
初期条件 $x(0)=0$ を用いると,$x$ 方向の位置は,
\begin{align}
x(t)=\frac{mv_0\cos{\varphi_0}}{\gamma}\left(1-\exp\left[-\frac{\gamma}{m}t\right]\right)
\end{align}
となります.
(3)$y$ 方向の運動方程式を解け.
\begin{align}
m\frac{dv_y(t)}{dt}&=-mg-\gamma v_y(t)
\end{align}
を変数分離法を用いて解きます.
左辺に $v_x(t)$ ,右辺に $t$ を集めると,
\begin{align}
\frac{dv_y(t)}{v_y(t)+\frac{mg}{\gamma}}&=-\frac{\gamma}{m}dt.
\end{align}
ここで,$\tilde{v}_y(t)=v_y(t)+\frac{mg}{\gamma}$ とおくと,
\begin{align}
d\tilde{v}_y(t)
&=d\left(v_y(t)+\frac{mg}{\gamma}\right)\notag\\
&=dv_y(t)
\end{align}
が得られます.
よって,運動方程式は,
\begin{align}
\frac{d\tilde{v}_y(t)}{\tilde{v}_y(t)}&=-\frac{\gamma}{m}dt
\end{align}
となります.
これは $x$ 方向の運動方程式と同じ形なので,先ほど求めた $v_x(t)$ の解において $v_x\to \tilde{v}_y$ に置き換えれば良いです:
\begin{align}
\tilde{v}_y(t)&=\tilde{v}_y(0)\exp\left[-\frac{\gamma}{m}t\right].
\end{align}
よって,$y$ 方向の速度 $v_y(t)$ は,
\begin{align}
v_y(t)
&=\left(v_y(0)+\frac{mg}{\gamma}\right)\exp\left[-\frac{\gamma}{m}t\right]-\frac{mg}{\gamma}\\
&=\left(v_0\sin{\varphi_0}+\frac{mg}{\gamma}\right)\exp\left[-\frac{\gamma}{m}t\right]-\frac{mg}{\gamma}.
\end{align}
また,$\tilde{v}_y(t)=v_y(t)+\frac{mg}{\gamma}$ の両辺を $t$ で積分すると,
\begin{align}
\tilde{y}(t)-\tilde{y}(0)=y(t)-y(0)+\frac{mg}{\gamma}t.
\label{y1}
\end{align}
一方で,$\tilde{y}(t)$ が $x(t)$ に対応するので,$x(t)$ の解を参照すると,
\begin{align}
\tilde{y}(t)-\tilde{y}(0)&=\frac{m\tilde{v}_y(0)}{\gamma}\left(1-\exp\left[-\frac{\gamma}{m}t\right]\right).
\label{y2}
\end{align}
\eqref{y1} と \eqref{y2} を比較すると,
\begin{align}
y(t)-y(0)+\frac{mg}{\gamma}t&=\frac{m\tilde{v}_y(0)}{\gamma}\left(1-\exp\left[-\frac{\gamma}{m}t\right]\right).
\end{align}
これを $y(t)$ について整理すると,
\begin{align}
y(t)&=\frac{m}{\gamma}\left(v_0\sin{\varphi_0}+\frac{mg}{\gamma}\right)\left(1-\exp\left[-\frac{\gamma}{m}t\right]\right)-\frac{mg}{\gamma}t.
\end{align}