目次
中心力の定義
質点に作用する力が常に空間内の一定点を向いていて,その大きさがその点からの距離のみによって決まるとき,この力を中心力と言います.
この定点を力の中心と言います.
例えば,太陽と地球からなる 2 体系を考えます.
太陽の質量は地球の質量よりも非常に大きいので,太陽のまわりの公転する地球の運動を解析する際には,太陽は不動とみなすことができます.
太陽の質量 $M_\odot = 1.989\times10^{30}\,\mathrm{kg}$,地球の質量 $M_\oplus = 5.972\times10^{24}\,\mathrm{kg}$ より,$M_\odot/M_\oplus\simeq 3.33\times10^{5}$ なので,約 33 万倍太陽の方が重いです.
太陽の位置を原点とすると,位置 $\boldsymbol{r}$ にある地球は太陽から次のような力を受けます:
\begin{align}
\boldsymbol{F}=-G\frac{M_\odot M_\oplus}{|\boldsymbol{r}|^2}\frac{\boldsymbol{r}}{|\boldsymbol{r}|}.
\end{align}
ここで,$G$ は万有引力定数です.
このような形で表される力を万有引力と言います.
これは地球(質点)から不動の太陽(一定点)を向いていて,その大きさは地球と太陽との間の距離 $|\boldsymbol{r}|$ にのみ依存するので,中心力であることがわかります.
中心力の一般論
中心力を定義したので,系に働く力が中心力のみの場合の一般論について議論します.
具体的には,
について扱います.
位置 $\boldsymbol{r}$ にある質点(質量 $m$ )が原点から受ける中心力を,
\begin{align}
\boldsymbol{F}=F(r)\frac{\boldsymbol{r}}{r},\quad r=|\boldsymbol{r}|
\end{align}
と表します.
角運動量保存則
質点が原点に対してもつ角運動量 $\boldsymbol{L}=\boldsymbol{r}\times\boldsymbol{p}$ の時間微分を考えます.
ここで,$\boldsymbol{p}=m\frac{d\boldsymbol{r}}{dt}$ は質点の運動量です.
角運動量の時間微分は,
\begin{align}
\frac{d\boldsymbol{L}}{dt}
&=\frac{d}{dt}(\boldsymbol{r}\times\boldsymbol{p})\\
&=\frac{d\boldsymbol{r}}{dt}\times\boldsymbol{p}+\boldsymbol{r}\times\frac{d\boldsymbol{p}}{dt}\\
&=\frac{d\boldsymbol{r}}{dt}\times m\frac{d\boldsymbol{r}}{dt}+\boldsymbol{r}\times \boldsymbol{F}\\
&=\boldsymbol{r}\times F(r)\frac{\boldsymbol{r}}{r}\\
&=\boldsymbol{0}
\end{align}
となります.
3 つ目の等号では,第 2 項に運動方程式を用いました.
そして,平行なベクトル同士の外積がゼロベクトルとなることを 4 つ目の等号と最後の等号で用いました.
この結果は,中心力のみが働く系において,力の中心まわりの角運動量が時間変化しない,つまり,角運動量保存則が成り立つことを意味しています.
あくまでも力の中心まわりの角運動量が保存するという主張であることに注意してください!
運動方程式
次に運動方程式について考えます.
先ほど示したように,原点(力の中心)まわりの角運動量は保存します.
一方で,角運動量の定義より,
\begin{align}
\boldsymbol{r}\cdot\boldsymbol{L}
&=\boldsymbol{r}\cdot(\boldsymbol{r}\times\boldsymbol{p})\\
&=0
\end{align}
が得られます.
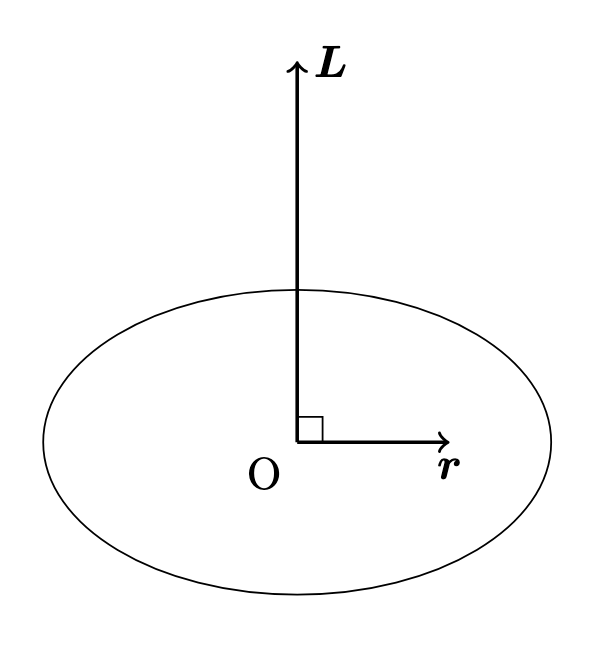
これらより,$\boldsymbol{r}$ は原点を通り,定ベクトル $\boldsymbol{L}$ に垂直な平面内に常に存在することがわかります.

その平面を $xy$ 平面に取り,2 次元極座標 $(r,\varphi)$ を考えます.
2 次元極座標における基底 $\boldsymbol{e}_{r}, \boldsymbol{e}_{\varphi}$ で位置 $\boldsymbol{r}$, 速度 $\boldsymbol{v}$, 加速度 $\boldsymbol{a}$ を展開すると,
\begin{align}
\boldsymbol{r}&=r\boldsymbol{e}_{r},\\
\boldsymbol{v}&=\frac{d\boldsymbol{r}}{dt}\\
&=\frac{dr}{dt}\boldsymbol{e}_{r}+r\frac{d\varphi}{dt}\boldsymbol{e}_{\varphi},\\
\boldsymbol{a}&=\frac{d\boldsymbol{v}}{dt}\\
&=\left[\frac{d^2r}{dt^2}-r\left(\frac{d\varphi}{dt}\right)^2\right]\boldsymbol{e}_{r}+\frac{1}{r}\frac{d}{dt}\left(r^2\frac{d\varphi}{dt}\right)\boldsymbol{e}_{\varphi}
\end{align}
となります.
また,中心力は,
\begin{align}
\boldsymbol{F}=F(r)\boldsymbol{e}_{r}
\end{align}
と書けます.
よって,運動方程式 $m\boldsymbol{a}=\boldsymbol{F}$ は,
\begin{align}
m\left\{\left[\frac{d^2r}{dt^2}-r\left(\frac{d\varphi}{dt}\right)^2\right]\boldsymbol{e}_{r}+\frac{1}{r}\frac{d}{dt}\left(r^2\frac{d\varphi}{dt}\right)\boldsymbol{e}_{\varphi}\right\}=F(r)\boldsymbol{e}_{r}
\end{align}
となります.
成分ごとに書くと,
\begin{align}
m\left[\frac{d^2r}{dt^2}-r\left(\frac{d\varphi}{dt}\right)^2\right]&=F(r),\\
\frac{m}{r}\frac{d}{dt}\left(r^2\frac{d\varphi}{dt}\right)&=0.
\end{align}
1 つ目が動径方向($r$ 方向)の運動方程式,2 つ目が方位角方向($\varphi$ 方向)の運動方程式です.