この記事では，力学で頻出する座標系について説明します．
2 次元座標系
2 次元空間の座標系としてよく使われるのは，次の 2 つです．
- 2 次元直交座標系
- 2 次元極座標系
直交座標系のことをデカルト座標（Cartesian 座標）と呼ぶこともあります．
Euclid 幾何学の問題を代数で扱う方法を体系化した René Descartes の名前をとってデカルト座標とも言います．また当時，学者名をラテン語化して表記する慣習があったため，カーテシアン座標とも言います．
2 次元直交座標系
2 次元直交座標系では，$x$ 軸と $y$ 軸を互いに直交するように取ります．
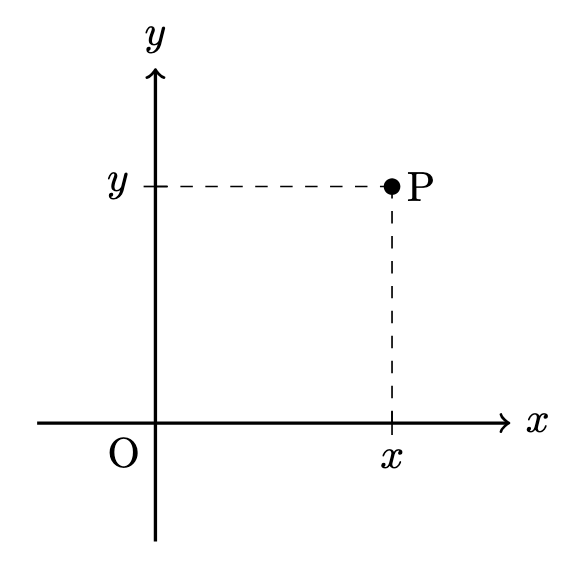
点 P の位置を $(x,y)$ と表します．
これは，以下の記事で解説した直交座標系の基底ベクトルを省略して，位置ベクトルの成分だけをまとめて表記したものと考えることができます．
高校のベクトルでよく見る表記法です！
2 次元極座標
円運動などを扱う際に便利な 2 次元極座標系を導入します．
2 次元極座標系では，原点から点 P までの距離 $r$ と，$x$ 軸とその直線のなす角 $\varphi$ で位置を表します．
この $r$ を動径，$\varphi$ を偏角と言います．
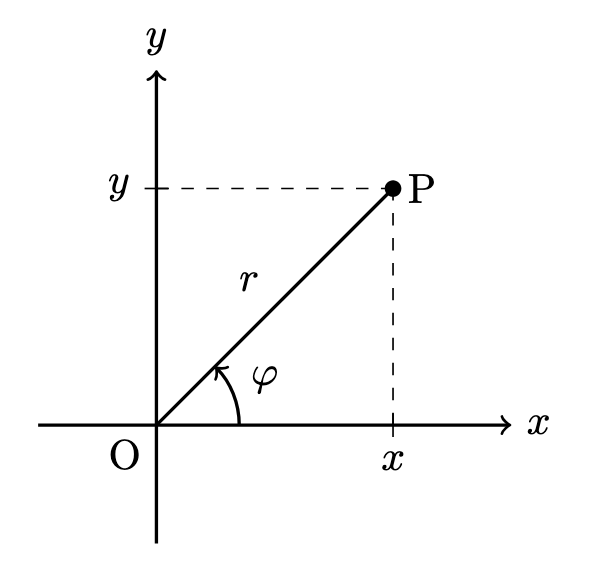
図より，2 次元直交座標系の成分 $(x,y)$ と 2 次元極座標系の成分 $(r,\varphi)$ は次の関係があることがわかります：
三平方の定理 $r^2=x^2+y^2$ が成り立つので，$r$ は，
$\tan{\varphi}=y/x$ より，$\varphi$ は，
$\arctan$ は $\tan$ の逆関数 $\tan^{-1}$ のことで，アークタンジェントと読みます．
3 次元座標系
3 次元空間の座標系としてよく使われるのは，次の 3 つです．
- 3 次元直交座標系
- 3 次元極座標系（球座標）
- 円柱座標系
通常，円柱座標系と言えば 3 次元座標系なので，3 次元円柱座標系とはあまり言いません
3 次元直交座標系
3 次元直交座標系では，三つの座標軸を互いに直交するように取ります．
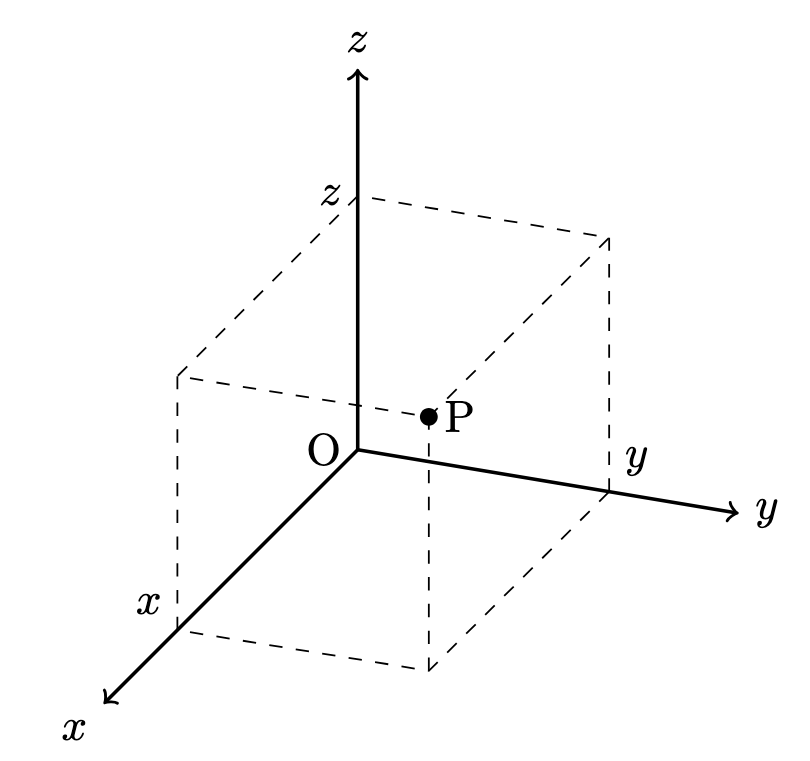
$x$ 軸，$y$ 軸，$z$ 軸の順に決めていくと，$z$ 軸の向きは 2 通り（上向きか下向きか）があります．
以下の記事で説明したように，上向きを正と取り，これを右手系と定義します．
3 次元極座標系（球座標）
3 次元極座標系では，原点から点 P までの距離 $r$，$z$ 軸とその直線のなす角 $\theta$，$x$ 軸とその直線の $xy$ 平面への射影のなす角 $\varphi$ で位置を表します．
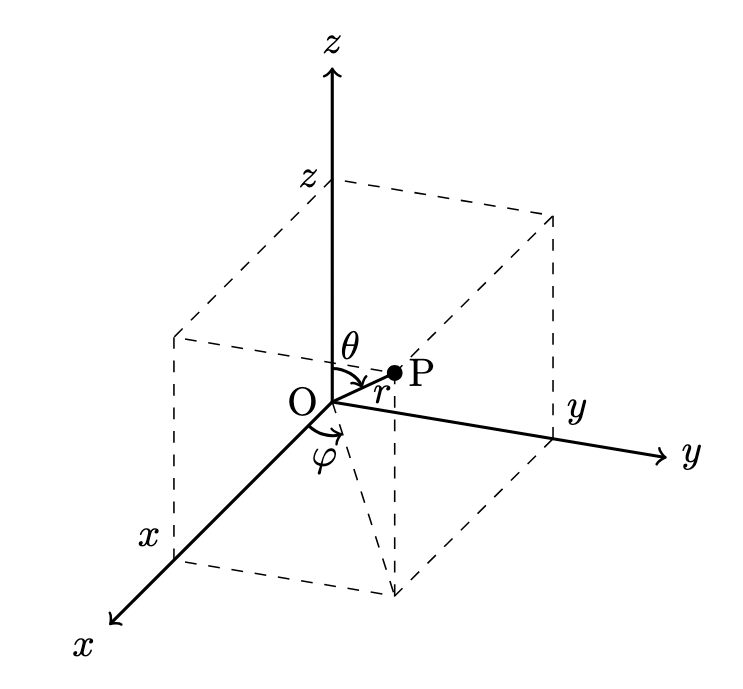
3 次元極座標系では， $r=\mathrm{const.}$ の面が球面を表すため，球座標とも呼ばれます．
図より，3 次元直交座標系の成分 $(x,y,z)$ と 3 次元極座標系の成分 $(r,\theta,\varphi)$ は次の関係があることがわかります：
$r^2=x^2+y^2+z^2$ が成り立つので，$r$ は，
$x^2+y^2=r^2\sin^2{\theta}$ と $z=r\cos{\theta}$ より，$\theta$ は，
$\tan{\varphi}=y/x$ より，$\varphi$ は，
円柱座標系
円柱座標系は，2 次元極座標系に $z$ 方向を加えた 3 次元座標系です．
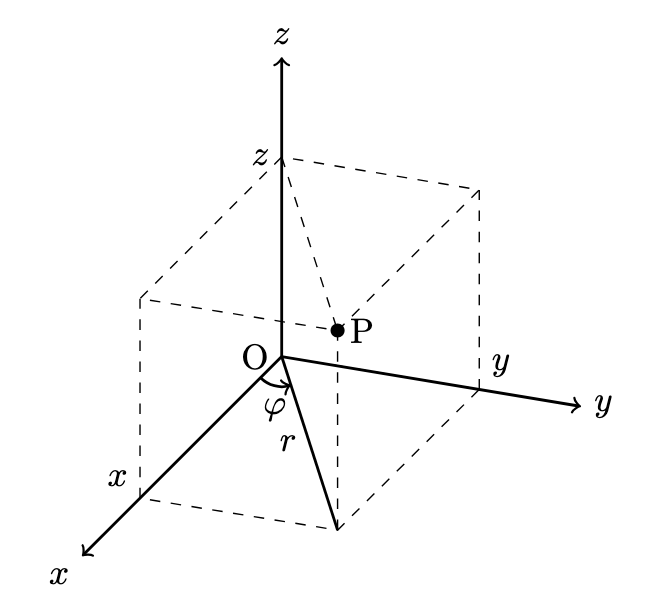
円柱座標系は，系が $z$ 軸まわりの対称性をもつときに便利です．
例えば，電磁気学における長い直線電流まわりの磁場，無限長ソレノイドの磁界などで現れます．
