以下の記事で,1 次元空間における位置・速度・加速度を導入しました.
この記事では,これらの量をベクトルで表現します.
また,2 次元空間,3 次元空間における位置・速度・加速度についても考えます.
最後にこれを任意の次元の空間に拡張します.
議論をする中で,直交座標系を導入します.
目次
位置ベクトル・速度ベクトル・加速度ベクトル
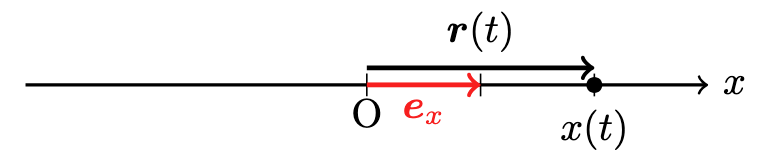
1 次元の場合
1 次元空間を運動する質点を考えます.
時刻 $t$ における質点の位置を $x(t)$ とすると,速度 $v(t)$ と加速度 $a(t)$ は,
\begin{align}
v(t)&=\frac{dx(t)}{dt},\\
a(t)
&=\frac{dv(t)}{dt}\\
&=\frac{d^2x(t)}{dt^2}
\end{align}
と表されます.
これらの量をベクトルで表現します.
1 次元空間内に適当に原点 O と選び,右向きを正とする $x$ 軸を取ります.
$x$ 軸の正の向きを向いた大きさ 1 のベクトルを $\boldsymbol{e}_x$ とすると,質点の位置は,
\begin{align}
\boldsymbol{r(t)}=\boldsymbol{e}_x x(t)
\label{position-vector}
\end{align}
のようにベクトルとして書くことができます.
この質点の位置を表すベクトルを位置ベクトルと言います.
また,大きさが 1 のベクトルを単位ベクトルと言い,$\boldsymbol{e}_x$ のように座標軸の正の向きを向いた単位ベクトルを基底ベクトルと言います.
速度が位置の時間微分で与えられるように,速度ベクトル $\boldsymbol{v}(t)$ は位置ベクトルの時間微分によって定義されます:
\begin{align}
\boldsymbol{v}(t)=\frac{d\boldsymbol{r}(t)}{dt}.
\end{align}
\eqref{position-vector} を代入すると,
\begin{align}
\boldsymbol{v}(t)
&=\frac{d}{dt}(\boldsymbol{e}_x x(t))\\
&=\frac{d\boldsymbol{e}_x}{dt}x(t)+\boldsymbol{e}_x\frac{dx(t)}{dt}\\
&=\boldsymbol{e}_x\frac{dx(t)}{dt}
\label{velocity-vector}
\end{align}
が得られます.
最後の等号で,基底ベクトル $\boldsymbol{e}_x$ が時間に依らないことを用いました.
同様に,加速度ベクトル $\boldsymbol{a}(t)$ は,
\begin{align}
\boldsymbol{a}(t)
&=\frac{d\boldsymbol{v}(t)}{dt}\\
&=\frac{d^2\boldsymbol{r}(t)}{dt^2}
\end{align}
で定義されます.
\eqref{velocity-vector} を代入すると,
\begin{align}
\boldsymbol{a}(t)
&=\frac{d}{dt}\left(\boldsymbol{e}_x\frac{dx(t)}{dt}\right)\\
&=\frac{d\boldsymbol{e}_x}{dt}\frac{dx(t)}{dt}+\boldsymbol{e}_x\frac{d^2x(t)}{dt^2}\\
&=\boldsymbol{e}_x\frac{d^2x(t)}{dt^2}
\end{align}
が得られます.
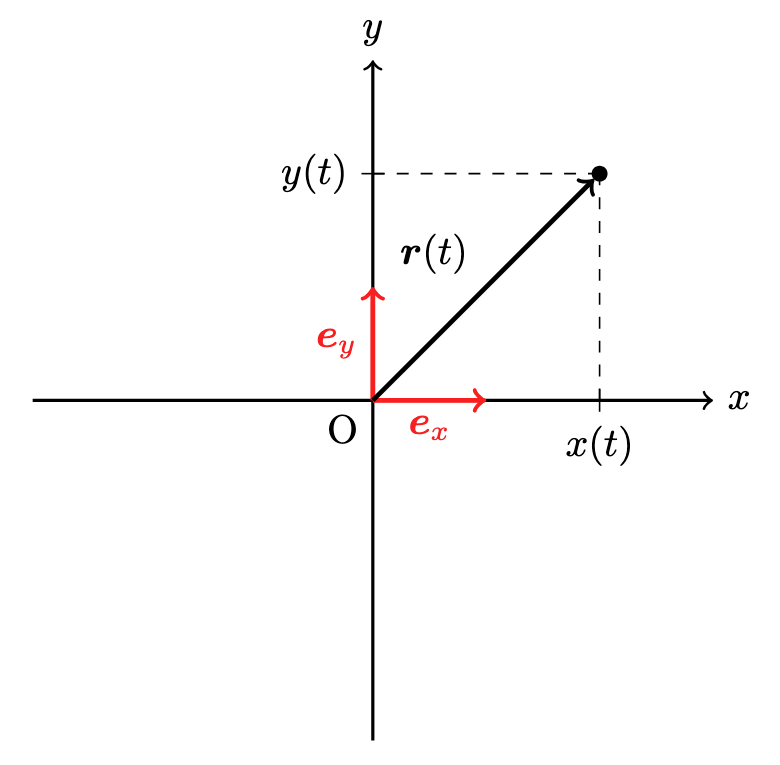
2 次元の場合
質点が 2 次元空間(平面)を運動する場合を考えます.
図のように原点 O を通り,$x$ 軸に直交するように $y$ 軸を取ります.
このような座標系を 2 次元直交座標系と言います.
$\boldsymbol{e}_x$ と同様に,$y$ 軸の正の向きを向いた大きさが 1 のベクトルを $\boldsymbol{e}_y$ と書きます.
$\boldsymbol{e}_x$ と $\boldsymbol{e}_y$ をまとめて,2 次元直交座標系における基底ベクトルと言います.
この基底ベクトルを用いると,質点の位置(位置ベクトル) $\boldsymbol{r}(t)$ は,
\begin{align}
\boldsymbol{r}(t)
=\boldsymbol{e}_xx(t)+\boldsymbol{e}_yy(t)
\end{align}
と表されます.
2 次元直交座標系の基底ベクトルは時間に依らないので,速度ベクトルと加速度ベクトルは,
\begin{align}
\boldsymbol{v}(t)
&=\frac{d\boldsymbol{r}(t)}{dt}\\
&=\boldsymbol{e}_x\frac{dx(t)}{dt}+\boldsymbol{e}_y\frac{dy(t)}{dt},\\
\boldsymbol{a}(t)
&=\frac{d^2\boldsymbol{r}(t)}{dt^2}\\
&=\boldsymbol{e}_x\frac{d^2x(t)}{dt^2}+\boldsymbol{e}_y\frac{d^2y(t)}{dt^2}
\end{align}
となります.
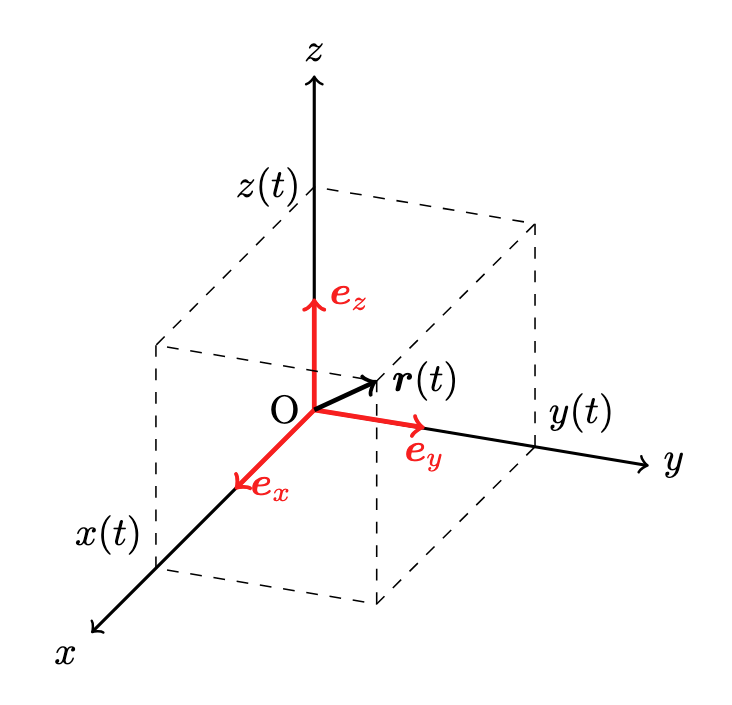
3 次元の場合
私たちが普段認識している空間は 3 次元空間なので,質点が 3 次元空間を運動する場合を考えます.
$xy$ 平面に直交するような $z$ 軸を考え,3 次元空間に図のように 3 次元直交座標系を取ります.
$x$ 軸から $y$ 軸に右ねじを回した時に,ねじの進む方向が正となるように $z$ 軸を取ります.
このように $z$ 軸を定めた 3 次元直交座標系を右手系と言います.
$z$ 軸の正の向きを逆向きに選ぶ座標系を左手系と言いますが,左手系を使うことはほとんどありません
3 次元空間中の質点の位置(位置ベクトル)は,
\begin{align}
\boldsymbol{r}(t)
=\boldsymbol{e}_xx(t)+\boldsymbol{e}_yy(t)+\boldsymbol{e}_zz(t)
\end{align}
と表されます.
ここで,$\boldsymbol{e}_z$ は $z$ 方向の基底ベクトルです.
$\boldsymbol{e}_x,\boldsymbol{e}_y,\boldsymbol{e}_z$ をまとめて,3 次元直交座標系における基底ベクトルと言います.
3 次元直交座標系の基底ベクトルは時間に依らないので,速度ベクトルと加速度ベクトルは,
\begin{align}
\boldsymbol{v}(t)
&=\frac{d\boldsymbol{r}(t)}{dt}\\
&=\boldsymbol{e}_x\frac{dx(t)}{dt}+\boldsymbol{e}_y\frac{dy(t)}{dt}+\boldsymbol{e}_z\frac{dz(t)}{dt},\\
\boldsymbol{a}(t)
&=\frac{d^2\boldsymbol{r}(t)}{dt^2}\\
&=\boldsymbol{e}_x\frac{d^2x(t)}{dt^2}+\boldsymbol{e}_y\frac{d^2y(t)}{dt^2}+\boldsymbol{e}_z\frac{d^2z(t)}{dt^2}
\end{align}
となります.
高次元の場合
これまで見てきた位置ベクトル・速度ベクトル・加速度ベクトルは,4 次元以上の高次元空間にも自然に拡張されます.
3 次元直交座標系における $x$ 軸,$y$ 軸,$z$ 軸という名前は,3 つの軸を区別できれば他の呼び方でも良いので,それぞれ 1 軸,2 軸,3 軸と呼ぶことにします.
また座標についても,$x(t)\to x_1(t),y(t)\to x_2(t),z(t)\to x_3(t)$ と置き換えます.
こうすると,位置ベクトルは,
\begin{align}
\boldsymbol{r}(t)
&=\boldsymbol{e}_1x_1(t)+\boldsymbol{e}_2x_2(t)+\boldsymbol{e}_3x_3(t)
\end{align}
と表されます.
これは和の記号 $\sum$ を用いて,
\begin{align}
\boldsymbol{r}(t)
=\sum_{i=1}^3\boldsymbol{e}_ix_i(t)
\end{align}
と書けます.
この表式を見ると,空間次元の数まで和を取っていることがわかります.
4 次元以上の空間に対しても,この位置ベクトルを次のように自然に拡張することができます.
$n$ 次元空間において,$n$ 次元直交座標系で位置ベクトルを表現すると,
\begin{align}
\boldsymbol{r}(t)
=\sum_{i=1}^n\boldsymbol{e}_ix_i(t)
\end{align}
となります.
速度ベクトル・加速度ベクトルは,
\begin{align}
\boldsymbol{v}(t)
&=\sum_{i=1}^n\boldsymbol{e}_i\frac{dx_i(t)}{dt},\\
\boldsymbol{a}(t)
&=\sum_{i=1}^n\boldsymbol{e}_i\frac{d^2x_i(t)}{dt^2}
\end{align}
となります.