【力学】自由度と座標系の導入

あらゆる物体は空間の中に存在し，時間の経過とともに一般には運動しています．

力学の基本的な目標の一つは，ある時刻における物体の状態（位置や速度など）をもとに，任意の時刻における運動を予測することです．

そのため，力学ではまず「物体の位置をどのように表すか」を考える必要があります．

物体の位置を一意に定めるために必要な独立な要素の数を自由度と呼びます．

座標を導入することで，この自由度を数値として扱えるようになります．

そして，空間内の任意の点に数値（座標）を割り当てるため枠組みを座標系と言います．

簡単な例

自由度や座標系といった概念に慣れるために，自由落下している物体を考えます．

力学では物体の大きさを無視することが多いので，ここでもそのように仮定します．

大きさの無視できる物体を質点（点粒子）と言います．

さて，自由落下している物体の位置をどのように表せば良いでしょうか？

例えば，各時刻における地面から測った高さがわかれば，この物体の位置が定量的に表現されたことになります．

この文章を分解すると，

のように考えていることがわかります．

一つ目がまさに自由度が 1 であることを表していて，二つ目と三つ目が座標系を定義しています．

すなわち，座標系は，基準（原点 O）と座標軸（$x$ 軸など）を選ぶことで定義されます．

ここで設定した座標系を用いて，物体の様子を図示すると以下のようになります．

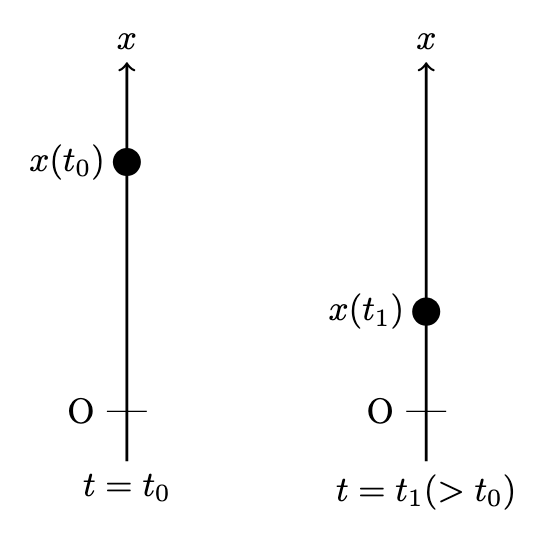
この座標系は，物体が落ちてくるのを真下から見上げていることに対応します．

原点 O には観測者がいると思えば良いです．

注意点

自由度と座標系に関する主な注意点は以下の 2 つです：

注意点 1：拘束条件がある際の自由度の数え方

一般に 3 次元空間の中を運動する物体の自由度は 3 です．

しかし，振り子やレールの上を走る電車のように，物体の運動が何らかの制約によって制限される場合があります．

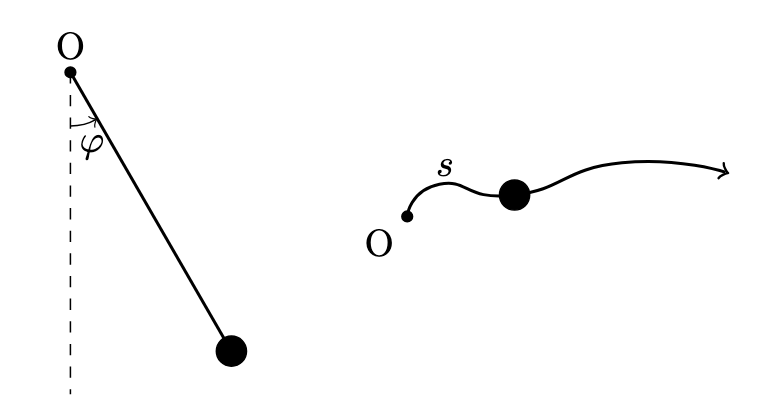
• 振り子：振り子の糸の長さが一定とすると，振り子の質点は円弧に沿ってしか動けません．この場合，物体の位置を決定するのに必要な自由度は 1 つで，それは角度 $\theta$ で表すことができます．
• 電車：電車はレールの上しか移動できません．電車はもちろん地面に拘束され，レールは一般に曲がっているため自由度が 2 のように見えます．しかし，座標系をレールに沿った変位 $s$として定義すれば，自由度は 1 となります．

注意点 2：物理現象は座標系に一切依存しないこと

物理現象は，どの座標系を選ぶかに関わらず本質的に同じ振る舞いを示します．

つまり，我々がどのような座標系を用いて解析しても，自然界で起こる現象そのものは変化しません，

その意味で座標系はあくまでその現象を記述・計算するための便宜的な手段にすぎません．

例えば，自由落下する物体の例では，地面に原点をとり，そこから鉛直上向きに $x$ 軸を取りました．

座標系は原点と座標軸，つまり，観測者がどの方向から物体の運動をみるかです．

落ちてくる物体を真下ではなく横から見たり，物体より高いところから見下ろして見ることも可能ですが，どこからどのように見たとしても，物体の落下運動そのものは変わりません．