現実のバネは調和振動子のように永遠に振動し続けるわけではなく,抵抗力により振幅は徐々に小さくなり,時間が経つと静止します.
このような振動を減衰振動と言います.
この記事では,減衰振動する系について扱います.
単振動(調和振動)については下記記事を参考にしてください.
減衰振動
運動方程式を立てる

質点に働く力として,バネによる復元力と質点の速度に比例した抵抗力を考えます:
ここで,$k$ はバネ定数,$\gamma$ は抵抗の比例係数です.(係数の 2 は計算のしやすさのために付けました.)
運動方程式は,
運動方程式を解く
運動方程式の両辺を $m$ で割り,左辺に集めると,
ここで,次のようにおきます:
すると,運動方程式は,
となります.
解の形を $x(t) = e^{\lambda t}$ と仮定して,運動方程式に代入すると,特性方程式
が得られます.
この $\lambda$ についての 2 次方程式を解くと,
$\zeta^2 – \omega_0^2$ が正かゼロか負かの 3 通りで解の振る舞いが変化します!
解の場合分け
減衰振動の場合
抵抗が小さく,$\zeta^2 – \omega_0^2<0$ を満たすときを考えます.
$\omega=\sqrt{\omega_0^2-\zeta^2}$ を導入すると,一般解は,
と書けます.($c_{1,2}$ は任意定数)
括弧内は下記記事で扱ったように単振動を表します.
よって,一般解は次のようにも書けます($A, \delta$ は定数):
単振動の解に $e^{-\zeta t}$ がかかっているので,振動の振幅は時間とともに指数関数的に減少していき,$1/\zeta$ 程度の時間スケールで大きく減衰します.
このような解の振る舞いを減衰振動と言います.
臨界減衰の場合
減衰振動より抵抗が大きく,$\zeta = \omega_0$ を満たす場合を考えます.
このとき,特性方程式 \eqref{characteristicequation} の解は,重解 $-\zeta$ となります.
よって,一般解は,
このような解の振る舞いを臨界減衰と言います.
過減衰の場合
臨界減衰よりもさらに抵抗が大きく,$\zeta^2 – \omega_0^2>0$ を満たすときを考えます.
このとき,$\sigma=\sqrt{\zeta^2 – \omega_0^2}$ とおくと,一般解は,
となります.
右辺の各項はどちらも振動する解ではなく,時間とともに単調減少する解です.
このような解の振る舞いを過減衰と言います.
解の様子
上記で示した 3 つの解の様子をグラフにすると、以下のようになります.
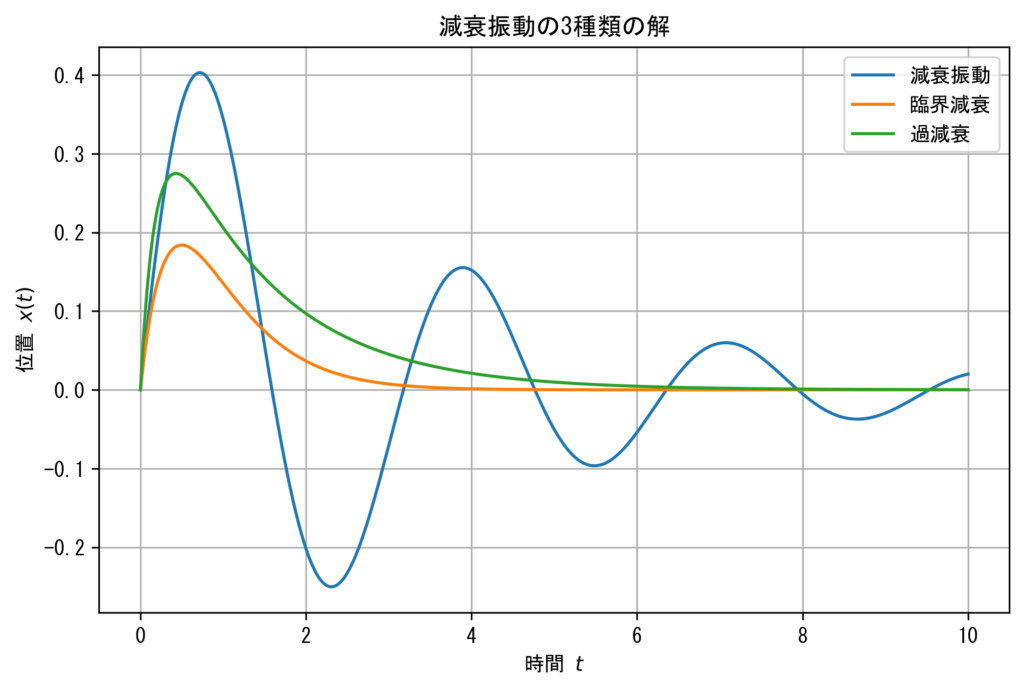

減衰振動は文字通り、振幅が時間とともに減衰しながら振動する解です.
抵抗力が大きくなり、臨界減衰と過減衰の振る舞いになると、もはや振動はせず、ゆっくりと\(x=0\)に減衰していく様子が読み取れます。








