この記事では,一様な重力のみが質点に働く場合の放物運動について扱います.
重力に加えて速度に比例した抵抗力も働く場合については,以下で扱っています.
目次
問題設定
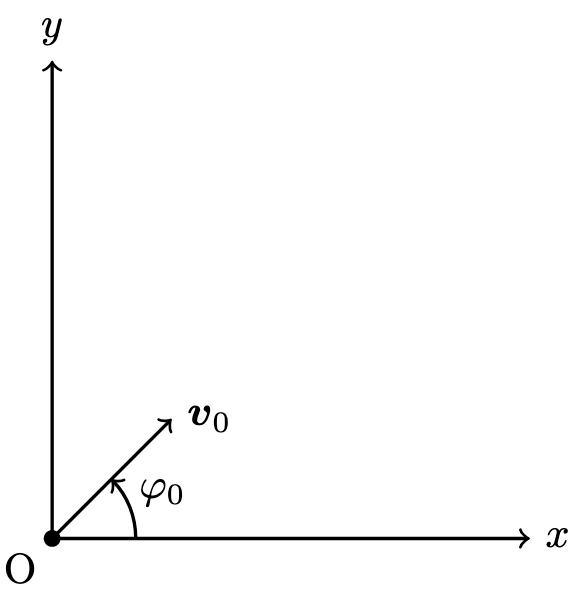
重力加速度を $\boldsymbol{g}$ ,その大きさを $g$ とします.
質点の質量を $m$ ,時刻 $t$ における位置を $\boldsymbol{r}(t)$ ,速度を $\boldsymbol{v}(t)$ とします.
座標系は図のように取ります.

このとき,ベクトル量を次のように成分表示します:
\begin{align}
\boldsymbol{g}&=(0,-g),\\
\boldsymbol{r}(t)&=(x(t),y(t)),\\
\boldsymbol{v}(t)&=(v_x(t),v_y(t)).
\end{align}
時刻 $t=0$ における初期条件は,
\begin{align}
\boldsymbol{r}_0&=\boldsymbol{r}(0)=(x(0),y(0))=(0,0),\\
\boldsymbol{v}_0&=\boldsymbol{v}(0)=(v_x(0),v_y(0))=(v_0\cos{\varphi_0},v_0\sin{\varphi_0}).
\end{align}
問題
(1)$x$ 方向,$y$ 方向の運動方程式をそれぞれ立てよ.
(2)$x$ 方向の運動方程式を解け.
(3)$y$ 方向の運動方程式を解け.
解答
(1)$x$ 方向,$y$ 方向の運動方程式をそれぞれ立てよ.
質点に働く力は重力のみなので,運動方程式は,
\begin{align}
m\frac{d\boldsymbol{v}(t)}{dt}=m\boldsymbol{g}.
\end{align}
鉛直上向きに $y$ 軸の正の向きを取っているので,重力は,
\begin{align}
m\boldsymbol{g}=(0,-mg)
\end{align}
となります.
よって,$x$ 方向,$y$ 方向の運動方程式はそれぞれ,
\begin{align}
m\frac{dv_x(t)}{dt}&=0,\\
m\frac{dv_y(t)}{dt}&=-mg
\end{align}
となります.
(2)$x$ 方向の運動方程式を解け.
\begin{align}
m\frac{dv_x(t)}{dt}&=0
\end{align}
を解きます.
両辺を $m$ で割り, $t$ で積分すると,
\begin{align}
\int_{0}^{t}\frac{dv_x(t’)}{dt’}dt’&=0\\
v_x(t)-v_x(0)&=0.
\end{align}
初期条件 $v_x(0)=v_0\cos{\varphi_0}$ を用いると,$x$ 方向の速度は,
\begin{align}
v_x(t)=v_0\cos{\varphi_0}
\end{align}
となります.
さらに,この式の両辺を $t$ で積分すると,
\begin{align}
\int_{0}^{t}v_x(t’)dt’&=v_0\cos{\varphi_0}\int_{0}^{t}dt’\\
x(t)-x(0)&=v_0\cos{\varphi_0}t.
\end{align}
初期条件 $x(0)=0$ を用いると,$x$ 方向の位置は,
\begin{align}
x(t)=v_0\cos{\varphi_0}t
\end{align}
となります.
(3)$y$ 方向の運動方程式を解け.
\begin{align}
m\frac{dv_y(t)}{dt}&=-mg
\end{align}
を解きます.
両辺を $m$ で割り, $t$ で積分すると,
\begin{align}
\int_{0}^{t}\frac{dv_y(t’)}{dt’}dt’&=-g\int_{0}^{t}dt’\\
v_y(t)-v_y(0)&=-gt.
\end{align}
初期条件 $v_y(0)=v_0\sin{\varphi_0}$ を用いると,$y$ 方向の速度は,
\begin{align}
v_y(t)=v_0\sin{\varphi_0}-gt
\end{align}
となります.
さらに,この式の両辺を $t$ で積分すると,
\begin{align}
\int_{0}^{t}v_y(t’)dt’&=\int_{0}^{t}(v_0\sin{\varphi_0}-gt)dt’\\
y(t)-y(0)&=v_0\sin{\varphi_0}t-\frac{1}{2}gt^2.
\end{align}
初期条件 $y(0)=0$ を用いると,$y$ 方向の位置は,
\begin{align}
y(t)=v_0\sin{\varphi_0}t-\frac{1}{2}gt^2
\end{align}
となります.